If you dip a wireframe into a soap solution it creates beautiful bubbles with all sorts of fascinating geometry as the bubble tries to minimize surface area. Watch the video or explore all the images below!
Tetrahedron
A tetrahedron wireframe has four vertices. It creates a bubble with planar surfaces that meet at a central vertex. If you then blow a bubble into the soap film, that central bubble mimics the boundary shape – a tetrahedral bubble inside a tetrahedral wireframe.


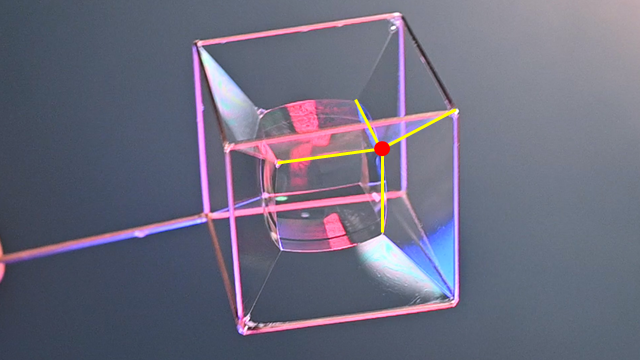
Cube:
A cube however doesn’t meet in a central vertex – it meets in a central square! If you shake the bubble up/down the square will face up. We get three orientations of this stable solution
If you blow a bubble into the center, it again mimics the boundary forming a central cube.



Octahedron
In addition to symmetry like the cube, the octahedron actually has five different interior configurations. The one with the smallest surface area makes a central tetrahedral vertex. However there are versions of a central hexagon facet, pentagon facet, square facet, and irregular quadrilateral facet.
As before, if you blow a bubble into the interior you get an octahedral bubble mimicking the boundary.




Plateau’s Laws
All these bubbles obey Plateau’s Laws:
- Lines are intersections of three planes with angle 120°
- Vertices are intersections of 4 lines with angle cos^(-1) (-1/3)≈109°
- Films are unbroken surfaces
- Mean curvature is everywhere constant
Check the bubbles above, notice how lines and vertices always obey these properties? These laws were proven mathematically by Jean Taylor using something called geometric measure theory.

One Boundary, Three Surfaces
This next wireframe creates three completely different surfaces.
- LEFT: The top loops are hollow and I can stick my finger through the center
- MIDDLE: The bottom loops are hollow and I can stick my finger through the cneter
- RIGHT: Both loops are hollow. This is topologically completely different, it is no longer even “simply connected”

Hole in a Plane
If you put a string in a plane and then pop it, the string forms a perfect circle! Why? A circle is the largest area for a fixed perimeter, so the bubble aiming to minimize surface area wants to subtract the largest area. This is analogous to why 3D bubbles form spheres when not attached to a boundary – a sphere has the minimal surface area for a given volume.


Bubbles on a Plane
Bubbles on a plane once again illustrate the 120 degree intersections of bubbles at every point of intersection. That the shapes on the plane minimize perimeter for two or three equal areas are actually theorems (Double Bubble Theorem is 1993, Triple Bubble Theorem is 2002, and amazingly the Quadruple Bubble Theorem wasn’t proven until 2021).


Bubbles Between Two Planes
We can see this even more clearly by putting bubbles between two planes. A single bubble forms a cylinder, once again leveraging the property that a circle minimizes surface perimeter for a fixed volume. A bunch of bubbles forms something like a honeycomb, with 120 degree angles everywhere. If I had done it with perfectly identical sized volumes not close to boundaries, it would actually make true regular hexagon tiling just like bees – bees are great minimizers!



Other cool bubbles!
Clockwise from top left:
- Mobius strip bubble – it has only one side!
- Trefoil Knot bubble
- Enneper’s Surface. If you extend the equations beyond the boundary you get a cool self intersecting surface; play with a demo of that here.
- Hopf Link. These are two linked circles and this type of surface is called a Seifert Surface
- Helicoid.
- Catenoid. You can actually derive the exact equation for this surface using something called the Calculus of Variation; check out my video on that here.





