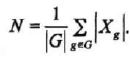There is a box containing “N” balls. Each ball has a number: bi; i from 1 to N.
Each ball is colored by one color, and there are “M” different colors. The number “bi” is equal to the number of balls whose color is as same as the color of the ith ball. For instance, if there are 4 red balls each red ball has the number 4.
If the summation of 1/bi from i=1 to N is 10, find M?
Although it is an easy puzzle, the idea of this puzzle is exactly that of counting orbits under a group action, which is presented by George Frobinous (it is usually referred to as Burnside’s Lemma).